(Solution) Number Line Jumps – HackerRank Problem Solving

Question

In this question, we’re given 4 numbers as input.

Let those 4 numbers be labeled x1, v1, x2, and v2 respectively.

In this case, x1 and x2 are starting positions of two kangaroos, say K1 and K2.

v1 and v2 are the distances that K1 and K2 cover at each jump respectively.

The task is to find out whether or not K1 and K2 will ever meet if they start jumping from x1 and x2 respectively.

Explanation With Example

Suppose, we get the following input: 0 3 4 2

In this case, x1 = 0, v1 = 3, x2 = 4, and v2 = 2.

Thus, the kangaroo K1 starts from 0 and after each jump, moves ahead by 3 meters. And, the kangaroo K2 starts from 4 and moves ahead by 2 meters.

Let’s tabulate the progress of each kangaroo at every jump to understand whether or not they’ll ever meet.

No. Of Jumps	Position Of K1	Position Of K2
0	0	4
1	3	6
2	6	8
3	9	10
4	12	12

Thus we can see that on the 4th jump, both the kangaroos K1 and K2 meet at the same position.

The same can be illustrated by the following image.

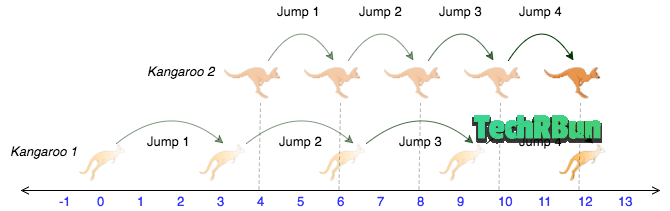
So in this case, the output should be “YES”.

Solution Explanation

Naive Solution

The most straightforward solution to this problem would be to run a while loop as long as the kangaroo which starts from a lesser value is at a position less than or equal to that of the kangaroo starting from a higher value, while both of them are jumping.

The code will look like this:

backwards_kangaroo = min (x1, x2)
forwards_kangaroo = max (x1, x2)
while (backwards_kangaroo <= forwards_kangaroo){
          make backwards_kangaroo jump
          make forwards_kangaroo jump
}
if backwards_kangaroo == forwards_kangaroo then "YES" else "NO"

However, this is not a good solution, and moreover, if the forwards_kangaroo covers more distance than the backwards_kangaroo at each jump, then the control will fall into an infinite loop. To prevent that, the following extra check must be added before the while loop.

if x2>x1 and v2>v1 then "NO"

Optimized Solution

To write the most optimized solution to this problem, let’s first form an equation with the given variables.

We have,

x1 = Starting position of kangaroo 1
v1 = Distance covered by kangaroo 1 in each jump
x2 = Starting position of kangaroo 2
v2 = Distance covered by kangaroo 2 in each jump

Let’s suppose that after N jumps, kangaroo 1 and kangaroo 2 meet.

Therefore we see,
starting position of kangaroo 1 + N times the distance covered by kangaroo 1 in each jump = starting position of kangaroo 2 + N times the distance covered by kangaroo 2 in each jump.

This is because we assume that both the kangaroos meet after each of them jumps N times.

Thus, we get the following equation:
x1 + N*v1 = x2 + N*v2

Let’s rewrite the equation to get the value of N.

x1 + N*v1 = x2 + N*v2
=> N*v1 – N*v2 = x2 – x1
=> N*(v1-v2) = x2 – x1
=> N = (x2 – x1)/(v1-v2) … (Required equation).

Now, this is only possible when N is a whole number, i.e. an integer that is greater than or equal to 0. This is because the kangaroos cannot jump backward (N < 0, rejected), and, the kangaroos cannot make partial jumps (N is strictly an integer).

Thus, we can calculate the value of N using the given input data, and if N is a whole number, we return “YES” otherwise, we return “NO”.

However, in case both the kangaroos start from the exact same point and cover the same distance in each jump, we can directly say that they will meet. Thus, we can directly return “YES” in that case.

In case only v1 == v2 (i.e., both kangaroos cover the same distance in each jump but do not start together), we can directly say that they will never meet as the distance between them is always constant. We have to check for this condition before the program tries calculating the value of N and returns “NO”. As otherwise, if the program tries to calculate the value of N in this case, the denominator becomes 0, and the “division by 0” exception will get raised.

Keeping the above points in mind, the optimized solution to the problem is given below. The solution is provided in Python, Java, C++, and C.

HackerRank Number Line Jumps: Python Solution

x1,v1,x2,v2 = list(map(int,input().split()))
if x1 == x2 and v1 == v2:
    print("YES")
    exit()
    
if v1 != v2:
    meet_point = (x2-x1)/(v1-v2)
    print("YES" if meet_point == abs(int(meet_point)) else "NO")
else:
    print("NO")

HackerRank Number Line Jumps: Java Solution

import java.util.Scanner;
class Solution{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int x1,v1,x2,v2;
        x1 = sc.nextInt();
        v1 = sc.nextInt();
        x2 = sc.nextInt();
        v2 = sc.nextInt();
        sc.close();
        
        if(x1 == x2 && v1 == v2)
            System.out.println("YES");
        else
            if(v1 != v2){
                float meet_point = (float)(x1-x2)/(v2-v1);
                if(meet_point == (int) meet_point && meet_point>0)
                    System.out.println("YES");
                else
                    System.out.println("NO");
            }
            else
            System.out.println("NO");
    }
}

HackerRank Number Line Jumps: C++ Solution

#include <iostream>
using namespace std;

int main(){
    int x1,v1,x2,v2;
    cin >> x1 >> v1 >> x2 >> v2;
    if(x1 == x2 && v1 == v2)
        cout << "YES";
    else
        if(v1 != v2){
            float meet_point = float((x2-x1))/(v1-v2);
            if(meet_point == int(meet_point) && meet_point>0)
                cout << "YES";
            else
                cout << "NO";
        }
        else 
            cout << "NO";
    return 0;
}

HackerRank Number Line Jumps: C Solution

#include <stdio.h>

int main(){
    int x1,v1,x2,v2;
    scanf("%d %d %d %d", &x1, &v1, &x2, &v2);
    if(x1 == x2 && v1 == v2)
        printf("%s","YES");
    else
        if(v1 != v2){
            float meet_point = (float)((x2-x1))/(v1-v2);
            if(meet_point == (int)(meet_point) && meet_point>0)
                printf("%s","YES");
            else
                printf("%s","NO");
        }
        else 
            printf("%s","NO");
    return 0;
}

Result

I hope I was able to explain the solution to the Number Line Jumps from HackerRank’s Problem Solving section.

If you have any doubts, feel free to comment down below. I will try my best to help you out.

FAQ