(Solution) Array Manipulation – HackerRank Interview Preparation Kit

Question

In this question, on the first line, we’re given two integers, say, ‘n’ and ‘m’.

Then, we’re given ‘m’ number of instruction-lines as input, in which each line contains 3 values.

We begin with a single-dimensional empty array ‘arr’ (all 0 values) of size ‘n’.

Note that the index of this array begins with 1, and not 0.

Each instruction-line has 3 values. The first two indicate two indices in the single dimensional array. Let’s call the three values on each line ‘a’, ‘b’, and ‘k’, respectively.

Our task is to add the ‘k’ of each instruction-line to every element of ‘arr’ belonging to an index ranging between the ‘a’ and ‘b’ of that particular ‘instruction line’.

The final task is to return the maximum value from the resultant array, i.e. ‘arr’.

I know this sounds very confusing, but the example given below will clear things up.

Explanation With Example

Suppose, we get the following input:

5 2
1 3 3
1 5 5

Here, n = 5 and m = 2. We start with a blank array ‘arr’ of size ‘m’, i.e. 5, {0, 0, 0, 0, 0} and perform the following tasks:

1. Add 3 to all the index positions between 1 to 3.
2. Add 5 to all the index positions between 1 to 5.

So, first of all let’s declare an array, arr = {0, 0, 0, 0, 0}

We do so because the value of n is 5.

Now, if we check the first instruction-line, we get {1, 3, 3}. According to the question, the first two values, i.e. 1, 3 are indices in whose range the third value, i.e. 3, must be added.

So, we add 3 to the values in 1, 2, and 3 index positions of arr.

Thus, arr becomes {0+3, 0+3, 0+3, 0, 0} = {3, 3, 3, 0, 0}

Next, if we check the second-instruction line, we get {1, 5, 5}. Which means, we must add 5 to the values of arr in indices which fall in the range of 1 to 5.

Thus, arr becomes {3+5, 3+5, 3+5, 0+5, 0+5} = {8, 8, 8, 5, 5}. This is the final resultant array.

The largest value in the resultant array is 8. Thus, 8 is the final answer.

Solution Explanation

Naive Approach

The most straightforward way of solving this problem would be to iterate through the instruction-lines one by one, and at each iteration, run an internal loop from ‘a’ to ‘b’ for that instruction-line and add the ‘k’ value to the values of arr at those indices. This approach would work exactly as shown in the above examples.

However, this approach would be too slow due to the presence of nested loops, and some of the larger test cases would throw a timeout error.

Thus, we need to solve this problem with a linear approach.

Optimised Approach

Instead of running an internal loop for the given range in each instruction-line and adding the ‘k’ value to each of those indices, we could simply add the ‘k’ value to the at the ‘a’th index and subtract the ‘k’ value from the ‘b’th index. And while finding the maximum value, we declare a max = 0 and a sum = 0 variable. We iterate through the resultant array and add each of its elements into the sum variable. At every iteration, we check whether the sum variable is bigger than the max variable or not. If yes, then we set max = sum.

Let’s understand this better with the help of an example.

Taking the same input as previously used:

5 2
1 3 3
1 5 5

We start with a blank array arr = {0, 0, 0, 0, 0}.

In the 1st instruction-line, a = 1, b = 3, and k = 3.

Thus, we put arr[a] = arr[a] + k and arr[b+1] = arr[b+1] – k.
Or, arr[1] = 0 + 3 = 3, arr[4] = 0 – 4 = -4.
arr = {3, 0, 0, -3, 0}

In the 2nd instruction-line, a = 1, b = 5, and k = 5.

Thus, we put arr[a] = arr[a] + k. But as arr[b+1] is arr[6], which is out of bounds, we do not take any further action.
Thus, arr[1] becomes arr[1] + 5 = 3 + 5 = 8.

We get the final resultant array as {8, 0, 0, -3, 0}.

We set max = 0, sum = 0.

Now we start iterating through the resultant array and adding its values in sum.

At index 1,
sum = sum + arr[1] = 8.
sum is greater than max. Thus max = sum = 8.

At index 2,
sum = sum + arr[2] = 8.
sum is not greater than max. Thus max stays the same.

At index 3,
sum = sum + arr[3] = 8.
sum is not greater than max. Thus max stays the same.

At index 4,
sum = sum + arr[4] = 5.
sum is not greater than max. Thus max stays the same.

At index 5,
sum = sum + arr[5] = 5.
sum is not greater than max. Thus max stays the same.

We return max (8) as the final answer.

Code Solution

The full code solution to the HackerRank Array Manipulation problem in Java and C++ are given below.

HackerRank Array Manipulation: Java Code Solution

import java.util.Scanner;
class Solution{
    public static void main(String[] args){
        long n, m, a, b, k, i, j, max = 0, sum = 0;
        Scanner sc=new Scanner(System.in);
        n = sc.nextLong();
        m = sc.nextLong();
        long arr[] = new long[(int) (n+1)];
        for(i=0; i<m; i++){
            a = sc.nextLong();
            b = sc.nextLong();
            k = sc.nextLong();
            arr[(int) a] += k;
            if(((int) (b+1)) <= n)
                arr[(int) (b+1)] -= k;
        }
        for(i=1; i<=n; i++){
            sum += arr[(int) i];
            max=Math.max(max, sum);
        }
        System.out.println(max);
    }
}

HackerRank Array Manipulation: C++ Code Solution

#include <iostream>
using namespace std;


int main() {
    long int n, m, a, b, k, i, j, max = 0,sum = 0;
    cin >> n >> m;
    long int *arr=new long int[n+1]();

    for(i=0; i<m; i++)
    {
        cin >> a >> b >> k;
        a[a] += k;
        if((b+1) <= n) 
            a[b+1] -= k;
    }

    for(i=1; i<=n; i++)
    {
       sum += arr[i];
       max = std::max(max, sum);
    }

    cout << max;
    return 0;
}

Result

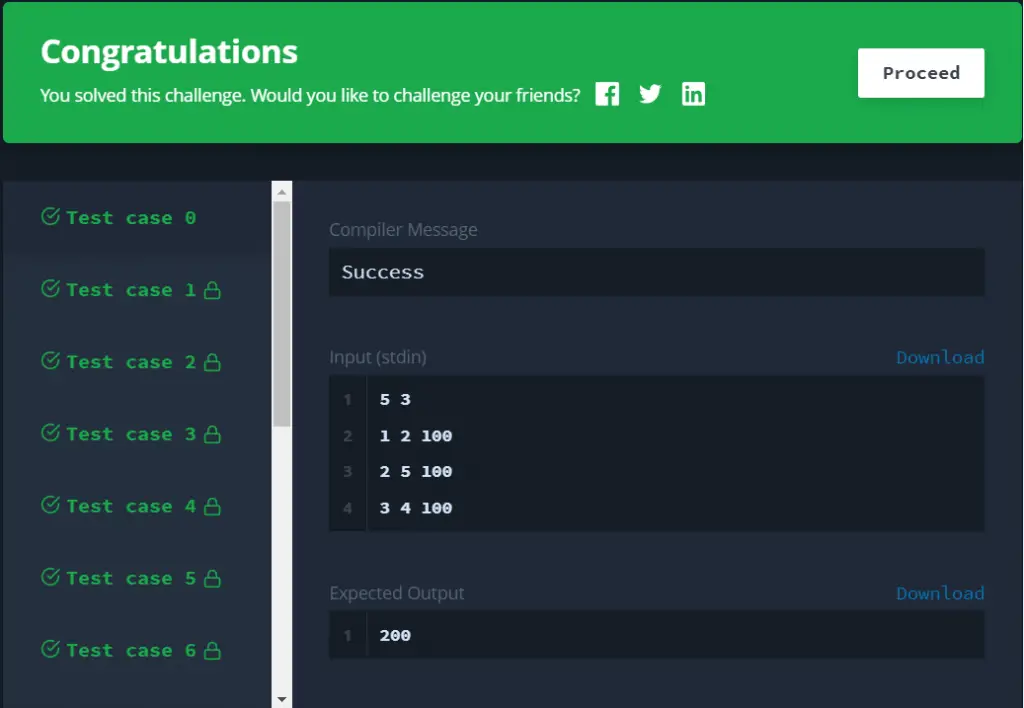
I hope I was able to explain the solution to the Array Manipulation problem from HackerRank’s Interview Preparation Kit.

If you have any doubts, feel free to comment down below. I will try my best to help you out.

FAQ